The Great Mystery of Deep Networks- Generalization

Introduction

In introductory statistics we are taught that our model should not overfit to the training set to avoid poor generalization and consequent poor test data performance. In line with this, some suggestions are to use a model with fewer parameters and also to consider explicit regularization of the weights, such as constraining the norm or the rank.

Yet the mystery is that these adages go out the window when it comes to deep networks. Over-parameterized deep networks with significantly more trainable parameters than there are training samples and with zero training loss still show great generalization to the test data. How is this possible? How are these over-parameterized and "over fitting" deep networks able to generalize?

Double descent: far enough into over-parameterized region, test performance increases

Implicit Regularization

Norm minimization

One hypothesis posits that generalization comes not from characteristics of the model class but rather from the optimization process.

Specifically, Gunaseka et al. 2017 (from TTIC with Nathan Srebo) states that in the linear network setting, gradient descent leads to a solution that has minimal nuclear norm (sum of singular values). More precisely, they assume gradient descent with infinitesimal step sizes (aptly termed gradient flow) and an initialization arbitrarily close to zero. They consider the matrix sensing optimization problem: we wish to recover some unknown matrix $W^*$ given some linear measurements $y_i = tr(A_i^T W^*) = <A_i, W^*>$ and given matrices $A_i$ .

In their set up they constrain the domain to the matrix factorization $W = U U^T$ . Gradient descent is then applied for the least squares minimization problem:

\min_{U} \sum_{i=1}^{m} (<A_{i}, U U^T> - y_{i})^{2}

What they show is that with a small enough initialization (this is key - it doesn't hold if the initialization is not small) and small enough steps sizes, gradient descent converges to a minimum nuclear norm solution, i.e., $\hat{W} = argmin_{L(W) = 0} ||W||_*$ . Thus gradient descent implicitly regularizes the model, where the regularization function is the nuclear norm $R = ||\cdot||_*$ .

Rank minimization

The norm minimization hypothesis has been disputed: Cohen et al. 2020, for example, gives counter-examples where with probability greater than 0.5 all norms blow up to infinity under gradient descent. What they show instead is that gradient descent tends to a minimum rank solution, suggesting that gradient descent minimizes rank instead of norm.

Li et al. 2021 also dispute the norm minimization thesis and affirm the rank minimization thesis with their work on Greedy Low Rank Learning (GLRL).

In fact, they prove that for the matrix factorization setting, their simple greedy algorithm GLRL is equivalent to gradient flow with an infinitesimal initialization.

In short, their algorithm GLRL starts with a matrix rank constraint of 1; they perform gradient descent and if it fails to reach a minimizer, they loosen the constraint by increasing the rank by 1 and they repeat this process until they reach a minimizing solution.

Non-linear networks?

So far we have only considered the setting of matrix sensing or matrix factorization problems, which is in the linear network setting.

But what about non-linear deep networks?

Unfortunately, the story is not so clear in the non-linear case. In fact, Vardi et al. 2021 show that even in a non-linear network with a single neuron, $x \to \sigma(<w,x>)$ , when the activation function $\sigma$ is RELU, we cannot express a non-trivial (in fact non-constant) implicit regularization function $R$ as a function of the parameters $w$ .

Non-infinitesimal initialization?

Even if we are interested in the linear network setting, in practice we might think that the assumption of an infinitesimal initialization is too restrictive for real applications. For example, a network with a RELU activation function cannot learn with zero initialized parameters as the gradient updates remain zero - and if the initialization is extremely close to zero, then learning will be inefficient as it may take a while to escape the saddle point near zero.

To overcome this restrictive infinitesimal initialization assumption, Zhao et al. 2023 propose a solution with their work InRank. They utilize the increasing rank idea from GLRL but they apply the rank constraint to not the weights themselves but the cumulative weight updates, i.e the weight matrices are $W = W_0 + D$ , where $D$ is the sum of weight updates. Moreover, they determine whether to increase the rank of the cumulative weight updates matrix based on an "explained ratio" metric which in essence measures for a rank $k$ constraint how well the first $k$ singular values explain the signal.

Incremental Learning

Another explanation for the generalization properties of deep networks may lie in incremental learning. Gissin et al. 2019 show that for matrix sensing and quadratic neural networks, under gradient flow the singular values of the parameters $W$ converge to the true value one at a time.

In short, this incremental convergence of singular values under gradient descent means that gradient descent finds solutions of increasing complexity, leading to generalization.

Unpacking this idea

One way to gain intuition is thinking about truncated singular value decomposition. We know from SVD any complex matrix $W$ can be decomposed into a sum of rank-1 matrices $\sum_{i=1}^{r} \sigma_{i} \boldsymbol{u}_{i} \boldsymbol{v}_{i}$ where $r$ is the rank of $W$ . Here, we can order the singular values by size, where $\sigma_{1} \geq \sigma_{2}... \geq \sigma_{r}$ . The idea behind truncated SVD is that the smaller singular values capture finer details while the larger singular values capture more broad stokes signals; thus by having the first $k < r$ singular values $\sum_{i=1}^{k} \sigma_{i} \boldsymbol{u}_{i} \boldsymbol{v}_{i}$ we get a coarse approximation of our matrix $W$ .

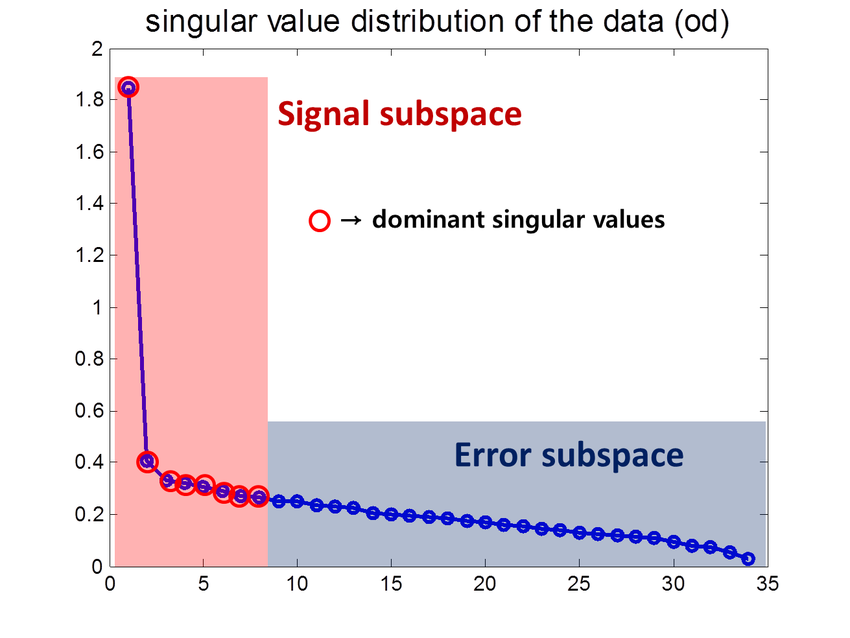
Singular Values

Singular values: large singular values capture signal, small singular values might capture noise

Back to our setting, since our model has the singular values converge one at a time, it initially only captures coarse signals but over time captures finer signals as the singular values converge. Solutions that gradually increase complexity tend to generalize better. To see this we might consider the filters in a CNN; the first few filters learn general broad strokes patterns and the later filters more precise patterns. This kind of coarse-to-complex learning allows for robustness, in comparison to a model that possibly learns/memorizes nuanced fine details (or noise) from the get-go from the training images, presenting a risk of bad overfitting.

CNN filters

CNN filter visualization: early filters detect broad patterns, later filters detect finer patterns

To summarize, incremental learning might explain the generalization properties of (certain) deep networks, because even though the hypothesis class (set of possible functions) of deep networks is huge, gradient descent finds solutions that increase in complexity gradually, which are better for generalization.